Gauge choices

Gauge conditions keep simulations from crashing and control the coordinates at future null infinity.

They determine the spacetime slices that the variables are evolved on. Usually, the distance between the slices (at constant time) is controlled by the lapse alpha, and the spatial coordinates are modified by the shift beta:

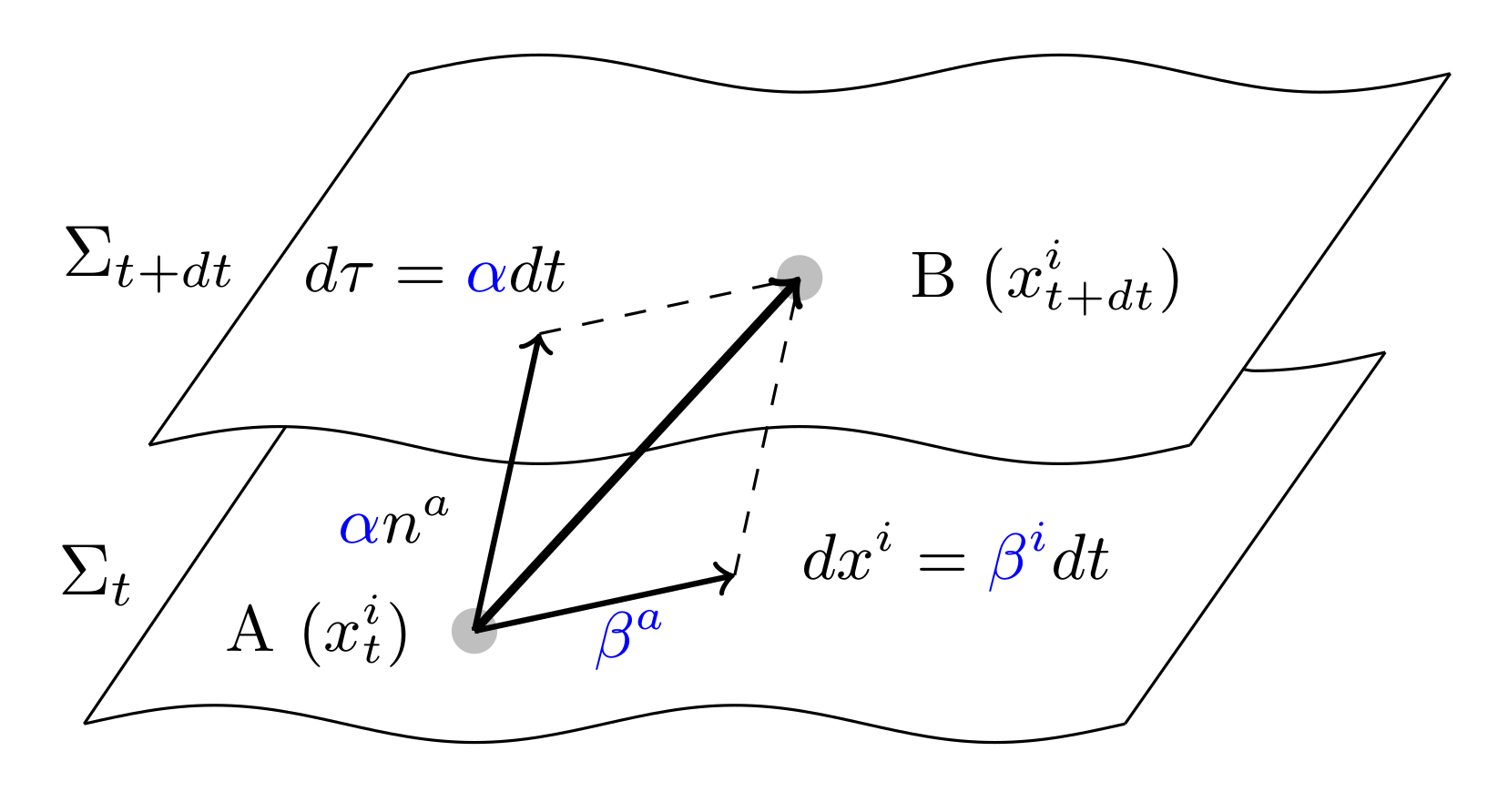
Slicing used in the common 3+1 decomposition of spacetime.

While some gauge choices have been designed in mind with the hyperboloidal approach in mind and others have been adapted experimentally, there is still much to be understood. A relevant effect to bear in mind is that the whole spacetime is affected by the choice of coordinates, which may have a deforming effect on the signals we want to measure. The following image (from 1705.06298 [gr-qc]) shows such effects, which need to be undone to obtain the correct signals. What we want here is to express our metric at future null infinity in Bondi-Sachs form.

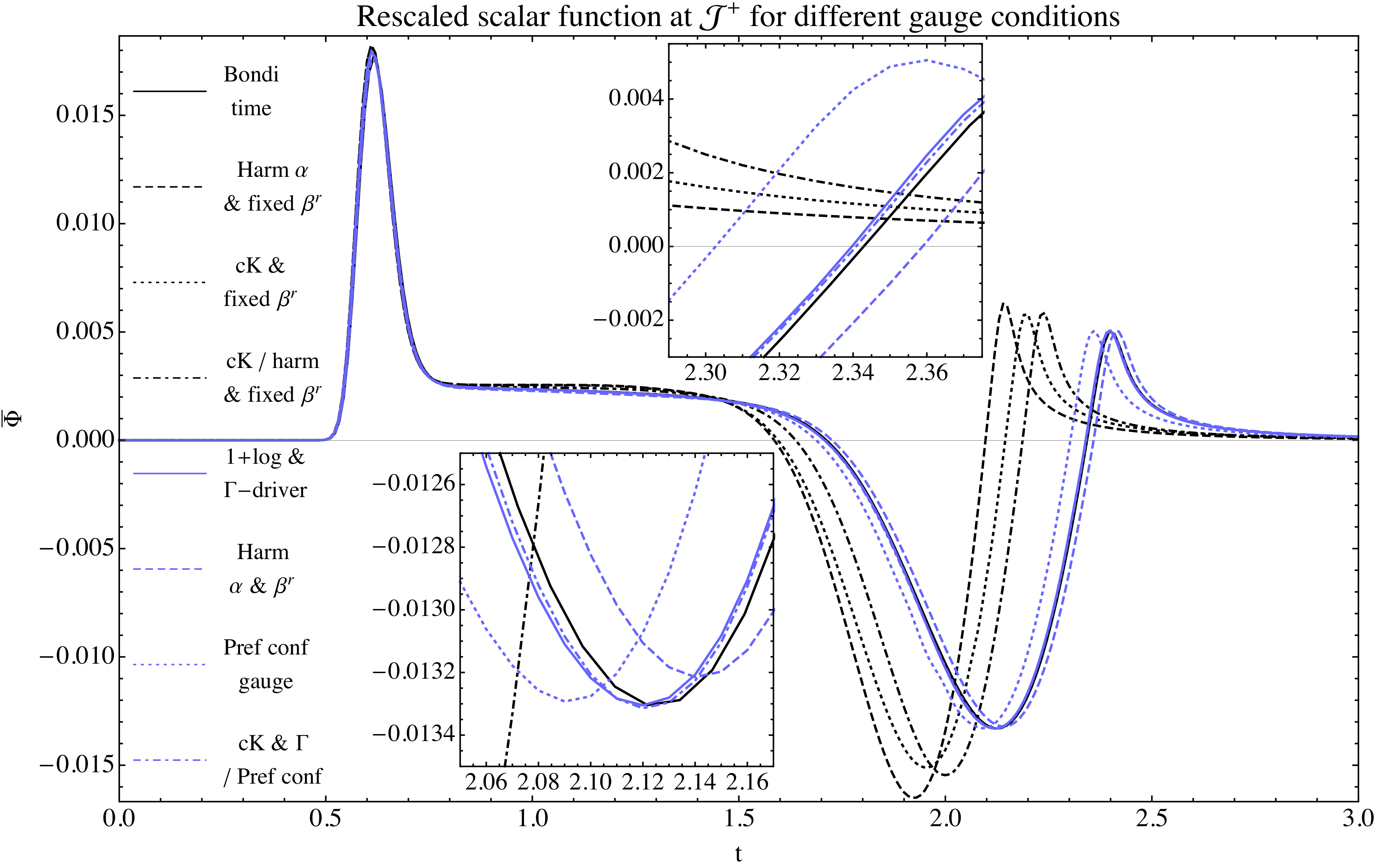
Deformed signals at future null infinity

Scalar field signals at future null infinity from a spherically symmetric hyperboloidal simulation. The different lines correspond to different choices of gauge conditions, which have different deforming effects on the signals.

Currently I am trying to better understand the degrees of freedom of the evolved gauge conditions at future null infinity. This will provide a way to generalise the conditions to ensure a clean treatment of the quantities there, so that their convergence can be ensured in the 3D simulations.

References

2018