Trumpet slices

Trumpets are slices of a black hole spacetime where inside of the horizon the proper length becomes infinite at a finite value of the (Schwarzschild-like) radial coordinate. Their embedding diagram (left image below) motivates their name. Especially interesting is the fact that trumpet slices avoid the black hole’s singularity, and so they can be used to reach inside of the black hole’s horizon.

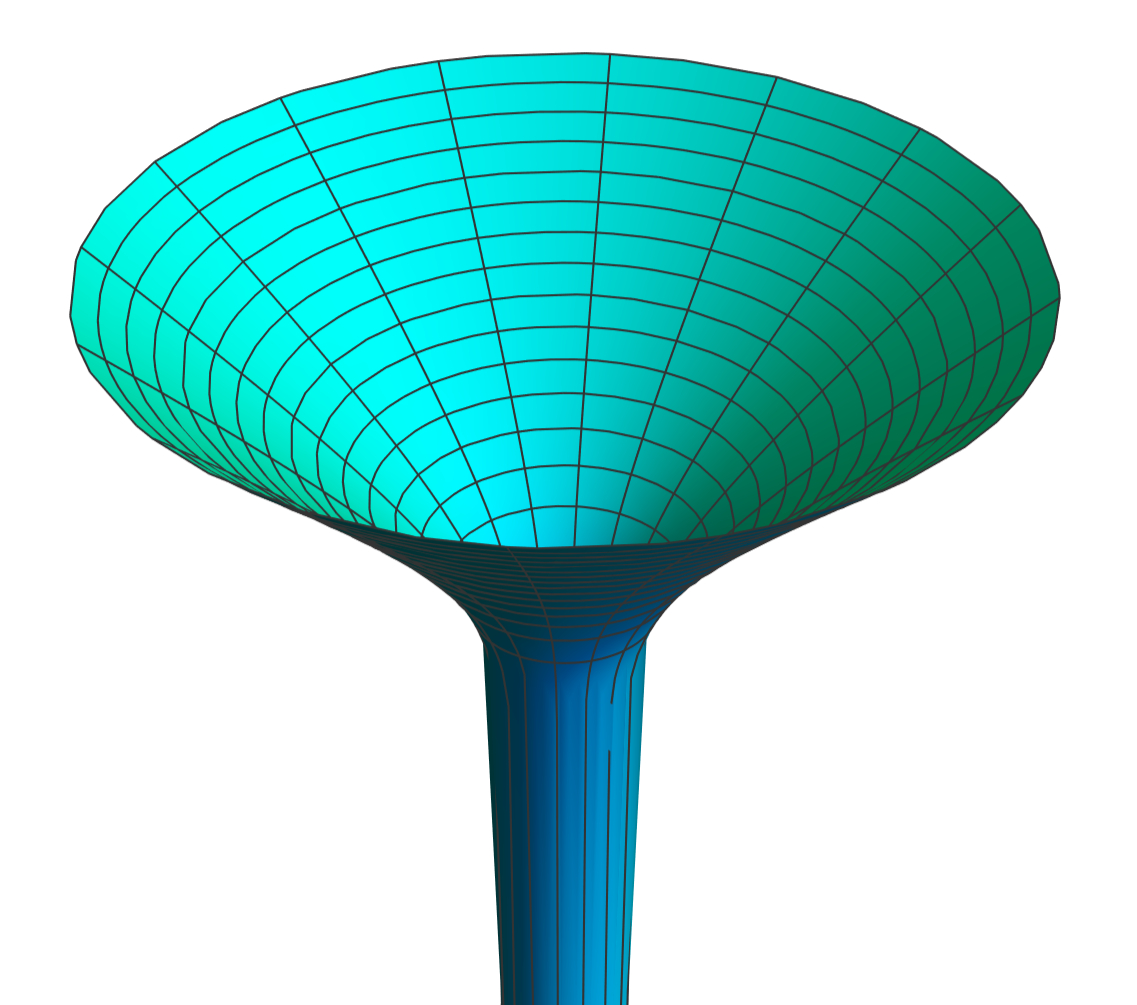
Embedding diagram of trumpet slices on the left, where the vertical axis shows the value of the proper length as a function of Schwarzschild radial coordinate and revolution angle. On the right, two different foliations (black and blue) of hyperboloidal trumpets of the Schwarzschild spacetime depicted on a Penrose diagram.

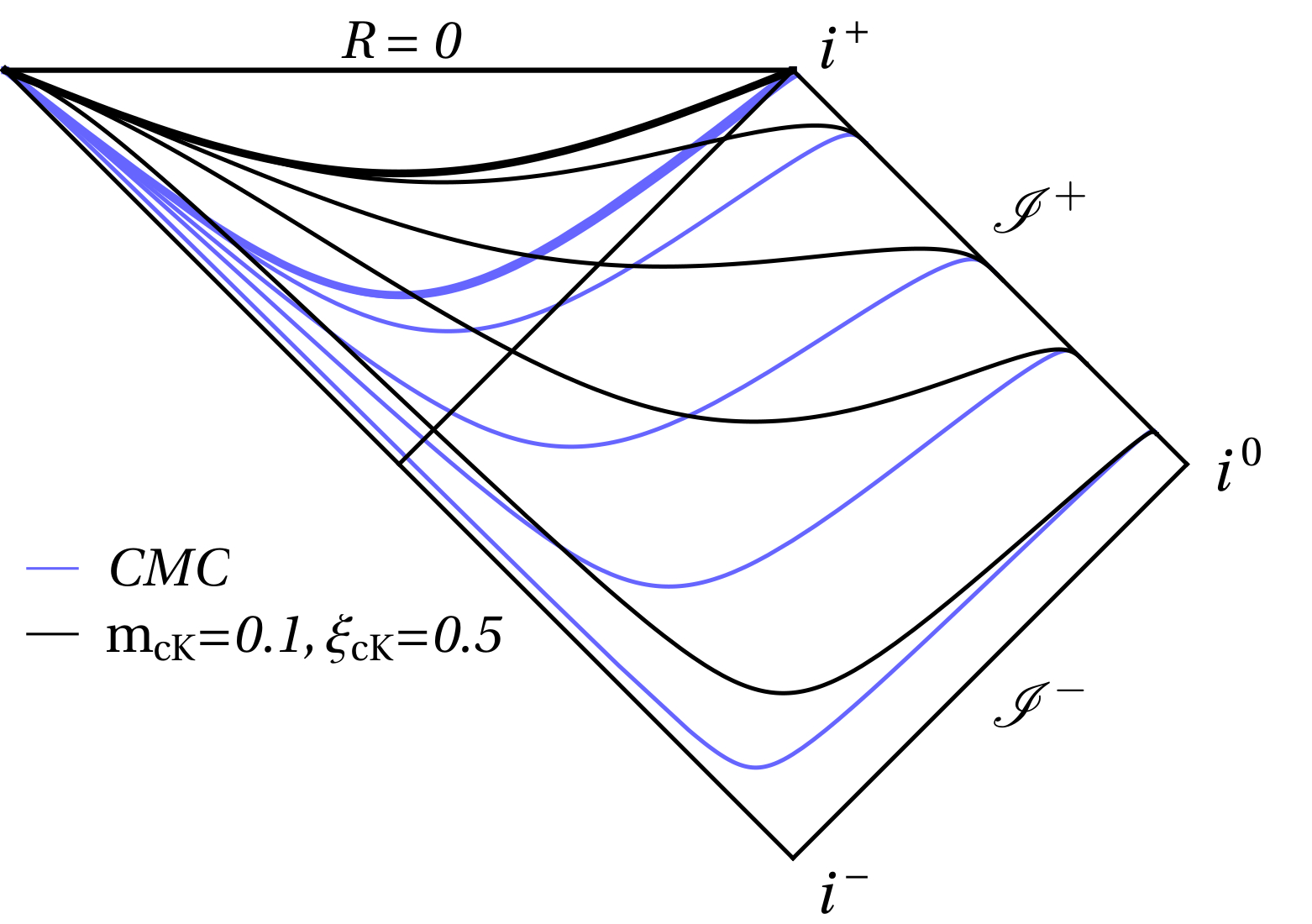
In 2304.05384 [gr-qc] I reviewed the construction of constant-mean-curvature trumpet slices of spherically symmetric black holes, and obtained similar Schwarzschild trumpets adapted to a specific choice of gauge.

I want to find out if an equivalent construction exists for Kerr (an axisymmetric black hole) and how to derive it. This will help when trying to construct a binary of spinning black holes!

References

2023